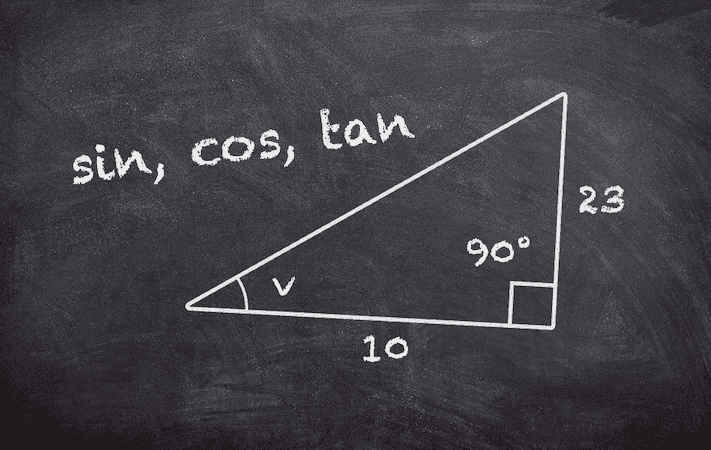Allt om sin, cos och tan

I den här artikeln beskriver vi allt om begreppen sin, cos och tan, eller sinus, cosinus och tangens.

De används inom trigonometrin i matematiken för att beräkna en rätvinklig triangels okända länger på sidorna och dess vinklar.

Sambanden mellan triangelns vinklar och sidor

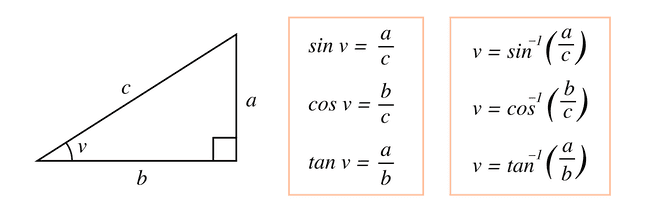
I bilden ovan beskrivs sambanden mellan den rätvinkliga triangelns olika sidor och vinkeln $v$. Här används begreppen $sin$, $cos$ och $tan$ för att beräkna någon av de okända sidorna $a$, $b$ eller $c$.

Uttryckligen brukar man säga “cosinus för vinkeln v” när man exempelvis talar om $\frac{b}{c}$.

Man kan även gå åt andra hållet för att beräkna vinkeln $v$ om den är okänd. Då behöver man känna till minst två av triangelns sidor för att sedan använda sig an inversen till sin, cos eller tan.

Man brukar skriva inversen till funktionerna som $\text{sin}^{-1}$, $\text{cos}^{-1}$ och $\text{tan}^{-1}$ eller $\text{arcsin}$, $\text{arccos}$ och $\text{arctan}$.

Sin, Cos och Tan

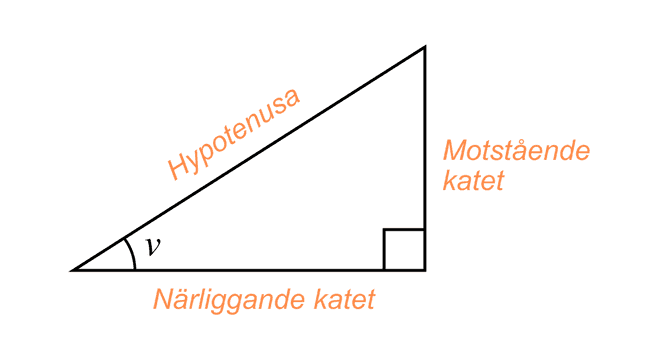
Här i bilen ovan syns de begrepp som används för att beskriva sidorna hos en rätvinklig triangel. De brukar även användas när man arbetar med Pyhtagoras sats, vilket du kan läsa mer om här.

Sin, Cos och Tan är funktioner som används för att ta reda på vinkeln v i triangeln och längden på triangelns sidor. Beroende på vilka av sidorna som är kända använder man någon av funktionerna för att beräkna vinkeln.

En kort repetition av begreppen för triangelns sidor:

1. Hypotenusan är alltid triangelns längsta sida, vilket även är den diagonala sida som ligger mittemot den räta vinkeln.
2. Den motstående kateten är den sida som befinner sig längst bort från vinkeln v. Man kan även säga att den ligger mittemot vinkeln v, vilket man hör lite på namnet.
3. Den närliggande kateten är den sida eller katet som ligger närmast vinkeln v, vilket man även hör lite på namnet.

Nedan följer nu beskrivningar på definitioner av sin, cos och tan när vi nu känner till namnen på triangelns sidor.

Sinus

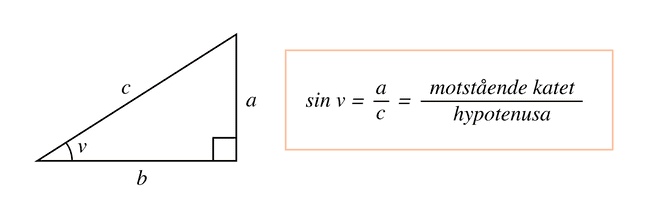
Med hjälp av sinus kan vi beräkna längden för antingen den motstående kateten eller hypotenusan om vi känner till vinkeln $v$.

Vi använder oss då av formeln ovan för att lösa ut antingen $a$ eller $c$.

På samma sätt kan vi med inversen för sinus, vilket betecnknas $arcsin$ eller $sin^{-1}$, även beräkna vinkeln $v$ om den är okänd.

För sin gäller alltså funktionerna:

$\text{sin } v = \frac{a}{c}$

$v = \text{sin}^{-1}(\frac{a}{c})$

Räkneexempel: sinus

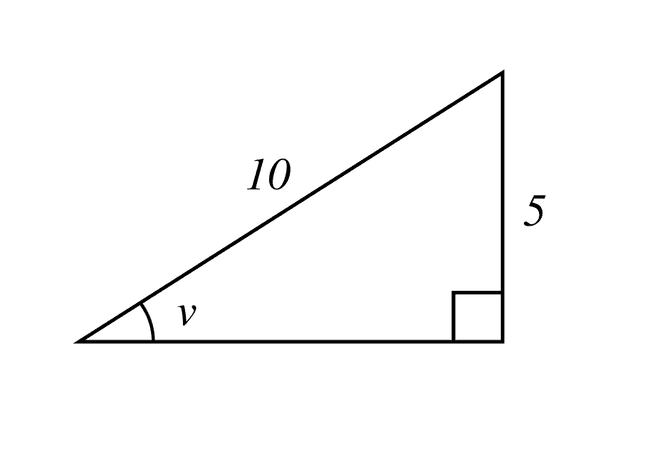
Bestäm vinkeln $v$ i den rätvinkliga triangeln.

I triangeln ser vi att längderna för den motstående katetern och hypotenusan är $5$ respektive $10$.

Det gör att vi kan använda oss av inversen av sinus för att bestämma vinkeln $v$ med formeln:

$v = \text{sin}^{-1}(\frac{5}{10})$

Om vi slår in HL på räknaren får vi att:

$v = 30°$

Svar: Vinkeln $v$ i triangeln är $30°$.

Cosinus

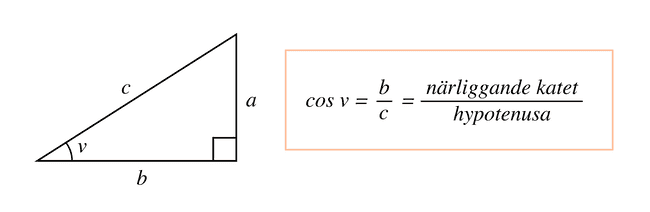
Med hjälp av cosinus kan vi beräkna längden för antingen den närliggande kateten eller hypotenusan om vi känner till vinkeln $v$.

Vi använder oss då av formeln ovan för att lösa ut antingen $b$ eller $c$.

På samma sätt kan vi med inversen för cosinus, vilket betecknas $arccos$ eller $cos^{-1}$, även beräkna vinkeln $v$ om den är okänd.

För cos gäller alltså funktionerna:

$\text{cos } v = \frac{b}{c}$

$v = \text{cos}^{-1}(\frac{b}{c})$

Räkneexempel: cosinus

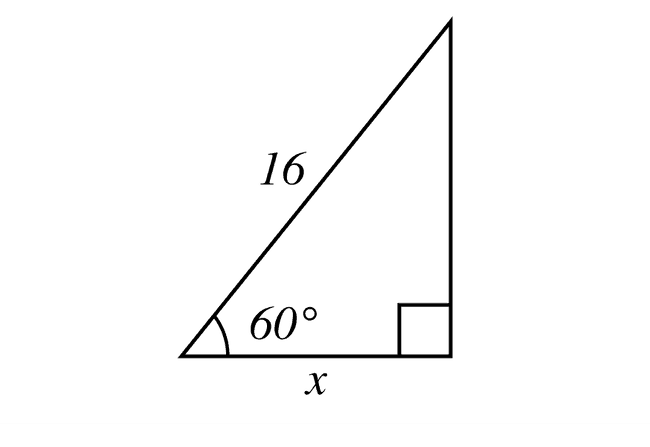
Beräkna längden för sidan $x$ i den rätvinkliga triangeln.

Vi ser att $x$ motsvarar den närliggande kateten och att hypotenusan har längden $16$ i vinkeln $60°$.

Då kan vi använda oss av formeln för cosinus på följande sätt:

$\text{cos }60° = \frac{x}{16}$

Först beräknar vi $\text{cos }60°$ på räknaren och får svaret $0,5$

Sedan löser vi ut $x$ genom stegen:

$0,5 = \frac{x}{16}$

$x = 8$

Svar: Längden för den närliggande kateten är $8$ l.e. (längdenheter)

Tangens

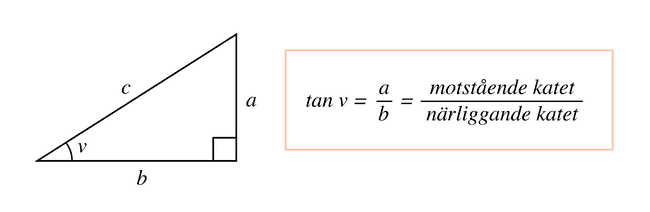
Med funktionen tangens kan vi beräkna längden för antingen den motstående eller närliggande kateten om vi känner till vinkeln $v$.

Vi använder oss då av formeln ovan för att lösa ut antingen $a$ eller $b$.

På samma sätt kan vi med inversen för tangens, vilket betecknas $arctan$ eller $tan^{-1}$, även beräkna vinkeln $v$ om den är okänd.

För tan gäller alltså funktionerna:

$\text{tan } v = \frac{a}{b}$

$v = \text{tan}^{-1}(\frac{a}{b})$

Räkneexempel: tangens

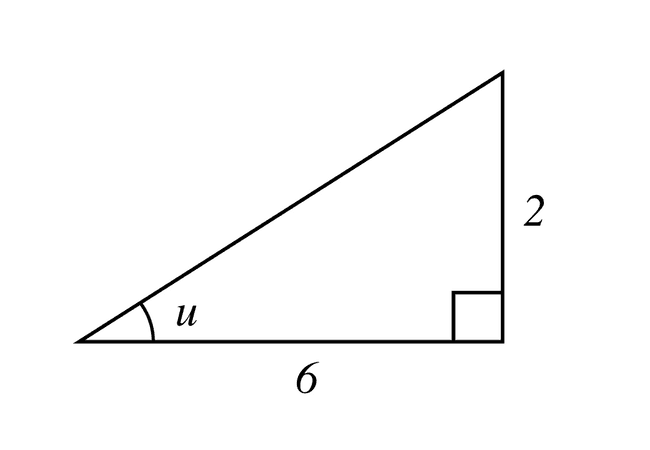
Beräkna vinkeln $u$ i triangeln givet sidorna med längderna 2 och 6.

I den här uppgiften har vi fått längden för de två katetrarna, vilket gör att vi kan använda oss av tangensinvers för att räkna ut vinkeln.

Det gör vi med den följande ekvationen:

$u = \text{tan}^{-1}(\frac{2}{6})$

Om vi slår in det på räknaren får vi svaret:

$u = \text{tan}^{-1}(\frac{2}{6}) ≈ 18,43°$

Svar: Vinkeln $u$ i triangeln är ungefär $18,43°$.